Die "Lösung" eines solchen Systems wird nach der Methode der sogenannten Kleinsten Quadrate bestimmt. Diese soll nun an einem Beispiel erläutert werden.

Jede Gleichung eines linearen Gleichungssystems kann man sich als Hyperebene vorstellen. Bei zweidimensionalen Problemen ist dies eine Gerade, bei dreidimensionalen Problemen eine Ebene und so weiter. Jeder Punkt, der auf der Hyperebene liegt, stellt damit eine Lösung der Gleichung dar. Der Schnittpunkt zweier Geraden, die Teil eines Gleichungssystems mit zwei Unbekannten sind, löst also beide Gleichungen. Demnach besitzt ein Gleichungssystem dann eine Lösung, wenn sich alle Hyperebenen in einem Punkt schneiden. Bei überbestimmten Gleichungssystemen ist das nicht mehr zu garantieren. Betrachtet man zum Beispiel

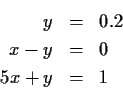
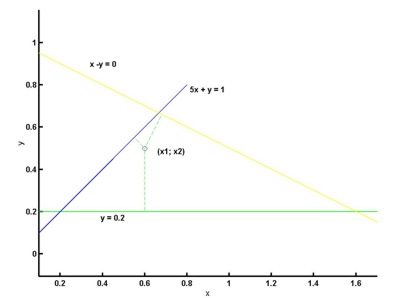
Abbildung 9: Graphische Darstellung des Beispiels

so erkennt man, daß keine Lösung existiert. Man kann aber für jeden Punkt (x1; x2) messen, wie "gut" dieser die Gleichungen erfüllt. Dabei ist 0.2-x2 der Fehler in der ersten Gleichung, 0 - x1 - x2 in der zweiten und 1-0.5 x1-x2 der Fehler in der dritten Gleichung. Um zu beurteilen, wie gut (x1; x2) alle drei Gleichungen erfüllt, verwenden wir als Maß r = (0.2-x2)²+(0-x1-x2)²+(1-0.5 x1-x2)². Offensichtlich gäbe es nur dann einen Punkt (x1; x2) mit r=0, wenn das Gleichungssystem eine Lösung besitzen würde. Da dies in unserem Beispiel nicht zutrifft, wollen wir (x1; x2) jetzt so wählen, daß r minimal ist. Es ergibt sich

x1 = 0.6 , x2=0.5

mit r = (-0.3)²+(-0.1)²+(0.2)² = 0.14. Für jeden anderen Punkt (x;y) ist r > 0.14.

Diese "optimale Lösung" bestimmt man durch das Lösen der Gaußschen Normalgleichungen. Schreibt man unser überbestimmtes Anfangssystem in der allgemeinen Form

Ax= b,

dann gibt es im allgemeinen kein x mit b-Ax = 0. Also bestimmen wir x so, daß der Residualvektor r = b-Ax eine möglichst kleine Länge besitzt. Gesucht ist ein Vektor x* für den Ax* nahe an der rechten Seite von b liegt.

Abbildung 10: Schema für die beste Näherungslösung

Die Abbildung 10 zeigt, daß die Lösung durch folgende Beziehung charakterisiert ist

(b - Ax*) ⊥ Ax (für alle x).

Dabei bedeutet v ⊥ w, daß die Vektoren v und w senkrecht aufeinander stehen. Diese Bedingung ist erfüllt, wenn das Skalarprodukt gleich Null ist, also für

A x • (b - A x*) = 0

Das Skalarprodukt zweier Vektoren x und y ist als Summe über die Produkte der Einzelkomponenten xi ·yi definiert: x • y = ∑ (i=1...n) xi ·yi. Damit kann es auch durch das Produkt der transponierten Matrix xT und y ausgedrückt werden: xT y = x ·y. Auf unsere ursprüngliche Forderung angewandt, ergibt sich

(A x)T (b - A x*) = 0

Nach dem Umstellen und Ausmultiplizieren erhält man xT AT (b - A x*) = 0 oder
xT (AT b - AT A x*) = 0. Diese Gleichung soll für alle x gelten, was äquivalent ist zu

AT b - AT Ax* = 0

Man erhält die Gaußsche Normalgleichung

AT A x* = AT b

Die Anzahl der Gleichungen dieses Systems entspricht der Anzahl der Unbekannten, da AT A eine quadratische Matrix ist. Damit kann man jetzt versuchen die Lösung zu bestimmen. Dieses x* erhält man durch x* = (AT A)-1 AT b. Außerdem ist zu erkennen, daß die Beziehung auch dann gilt, wenn das ursprüngliche System Ax = b lösbar ist. In diesem Fall ergibt sich die exakte Lösung.

Durch die Gaußsche Normalgleichung haben wir eine Möglichkeit, das überbestimmte Gleichungssystem zu lösen. Es zeigt sich jedoch, daß diese Methode nicht immer den effizientesten Ansatz darstellt.

Abbildung 11: Besetzung des Gleichungssystems

Wie zu erkennen ist, besitzt die Ausgangsmatrix A nur 22083 von Null verschiedene Einträge, während AT A 115640, also mehr als fünf mal so viel solche Einträge beinhaltet. Das führt zu erheblichen Speicherproblemen, sobald größere Matrizen gewählt werden. Außerdem hat die Lösung von AT A x* = ATb durch Gaußelimination eine Komplexität von dim(A)3, was im Beispiel etwa 64 Millionen Rechenoperationen erfordert.
Man ist bemüht Verfahren zu finden, die ohne Verwendung der Normalgleichung direkt mit A operieren und dabei die senkrechte Beziehung ausnutzen. Interessant sind Algorithmen bei denen die Koeffizientenmatrix A nur über Matrix-Vektor-Operationen eingeht. Dies führt zu Iterationsverfahren, bei denen ausgehend von einem Startwert x0 sukzessive bessere Näherungen x1,x2,x3,x4 berechnet werden, wobei die wesentliche Operation beim Übergang von xn zu xn+1 eine Multiplikation mit A ist. Ein solches Verfahren ist zum Beispiel das Kaczmarz-Verfahren.

Vor allem die folgenden wären dabei zu erwähnen:

• die mit der Auswertung verbundene Rechenzeit - hauptsächlich für die Lösung des Gleichungssystems. Zum Lösen dieses Problems kann man zum Beispiel auf die schon angesprochenen Iterationsverfahren zurückgreifen.
• die Auswirkungen von (kleinen) Meßfehlern bei inversen Problemen. Zur Untersuchung der möglichen Effekte können kleinere Meßfehler simuliert und die gewonnenen Ergebnisse ausgewertet werden. Daraus lassen sich dann Möglichkeiten zur Reduzierung des Effektes erarbeiten.
  Die Abildungen 14 und 15 zeigen in dem Zusammenhang die rekonstruierten Bilder bei einem simulierten Fehler von etwa 3 Prozent. In beiden Fällen wurde das Ausgangsphantom von Abbildung 12 mit einer Größe von 20×20 verwendet. Zur Erzeugung von Bild 14 setzten wir 60 Schritte ein, was einer Anzahl von 540 Gleichungen entspricht, und bei Bild 15 wurden 90 Schritte mit 810 Gleichungen benutzt.