Die Röntgenstrahlen sollen von einer Röntgenquelle Q ausgesandt werden, die sich im Abstand r zum Ursprung bewegt. Bei jeder Messung wird ein Bündel an Röntgenstrahlen emittiert, wobei die Auslenkung eines Strahles zum Zentralstrahl beträgt. Dieser verläuft unter dem Winkel vom Punkt Q aus durch den Koordinatenursprung. Die Strahlen treten auf der einen Seite in das Phantom ein und treffen auf das Sensorfeld, welches der Röntgenquelle gegenüberliegt. Das Material außerhalb des Körpers soll den Röntgenstrahl nicht schwächen, was bei geeigneter Eichung auch praktisch umsetzbar ist.

Das folgende Schema zeigt noch einmal den grundlegenden Aufbau und relevante Größen:

Abbildung 5: Aufbau des Modells

Pro Durchlauf sollen step Messungen durchgeführt werden, das heißt die Quelle und die gegenüberliegenden Sensoren werden um den Winkel weiterbewegt. Besteht ein Strahlenbündel aus a Strahlen, dann werden insgesamt a ·step Messungen erfaßt.

• der Index der getroffenen Pixel, das heißt ihre Position im Phantom,
• die Länge der durchlaufenen Strecke in jedem Pixel.

Der Algorithmus zur Berechnung wurde im Programm »spunkt.m« (vgl. A.1) umgesetzt und soll im Folgenden beschrieben werden.

Für die weiteren Betrachtungen werden zunächst die Schnittpunkte der Strahlen mit dem Gitternetz benötigt. Hierzu wird für jeden Strahl, der durch 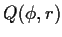und a gegeben ist, eine Punkt-Richtungs-Gleichung aufgestellt:

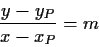
Wobei xP und yP die Koordinaten eines durchlaufenen Punktes und m der Anstieg der Geraden ist. Diese Steigung m ergibt sich aus m = tan(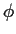+ 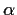). Nach dem Umstellen von (3) erhält man für y:

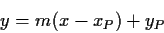
Und für x:

Nach dem Einsetzen von y = -n, ..., n in (5) ergeben sich die jeweiligen Schnittpunkte mit den vertikalen Achsenparallelen.

Diese Schnittpunkte werden in der Matrix X_S abgelegt. Die Spalten in der Matrix enthalten die x-Koordinate des Schnittpunktes eines Strahls. Um die Längen effizient berechnen zu können, ist eine aufsteigende Sortierung nach den x-Werten (X_S) und eine entsprechende Ermittlung der zugehörigen y-Werte(Y_S) nötig. Dazu werden die x-Koordinaten in eine weitere Matrix P_X übertragen und die Werte x = -n, ..., n ergänzt. Anschließend kann P_X aufsteigend in die Matrix S_X sortiert werden. Durch Einsetzen dieser Werte in (4) erhält man in der Matrix S_Y die entsprechenden y-Koordinaten. Matlab macht es möglich die Schnittpunktsberechnungen simultan für das gesamte Strahlenbündel durchzuführen, weshalb die Spaltenanzahl der Matrizen S_X und S_Y mit der Anzahl der Strahlen im Bündel übereinstimmt.

Die Indizes durchlaufener Pixel, das heißt die Positionen im Phantom, sind wichtig um später auf die richtigen Schwächungskoeffizienten zugreifen zu können. Zuerst werden für die getroffenen Pixel ,,Phantomkoordinaten'' ausgerechnet. Dieses gedachte Koordinatensystem beginnt in der linken unteren Ecke mit dem Pixel (1,1); siehe dazu Abbildung 6. Um die Koordinaten zu erhalten wird der Mittelwert von zwei aufeinanderfolgenden Schnittpunkten der jeweiligen x- bzw. y-Werte gebildet, n addiert und anschließend auf die nächstgrößere ganze Zahl gerundet. Daraus kann nun der Index mit der Formel i = (x + y ·2 ·n)-2 ·n berechnet werden. Allerdings ist es möglich, daß Pixel auch außerhalb des Phantoms liegen, nämlich dann wenn x < 1 oder x > 2 ·n ist (analoges gilt für y). Dieser Effekt entsteht durch das Schneiden von -n bis n. Sinnvollerweise werden diese Pixel bei den weiteren Betrachtungen ignoriert. Daher speichern wir die Koordinaten der entsprechenden Pixel und setzen die jeweiligen Indizes auf einen "harmlosen" Wert, wie zum Beispiel 1.

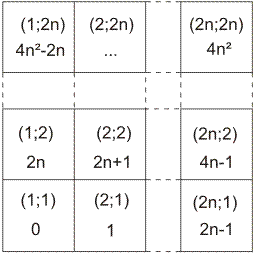
Abbildung 6: Schema zur Indexberechnung

Eine Strecke zwischen zwei Punkten A und B läßt sich mit Hilfe des Satzes des Pythagoras errechnen, es gilt: 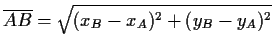. Nach Einsetzen der Schnittpunktskoordinaten in die obige Formel und Aussortieren außenliegender Pixel durch Nullsetzen der Länge, liegen die durchlaufenen Strecken in den einzelnen Pixeln des Phantoms von links nach rechts vor.

Datenorganisation

Als erstes muß eine effiziente Abstrahierung der vorhandenen Daten diskutiert werden. Besonders die Fähigkeiten der Matrizenmanipulation des Programmes Matlab sollten dabei zum Zug kommen. Da für das Phantom eine quadratische Form gewählt wurde, kann man die Schwächungskoeffizienten in einer 2n×2n Matrix anordnen:

Die Indizes an den Koeffizienten geben die Phantomkoordinaten an. Um aber nicht beide Koordinaten speichern zu müssen, wandeln wir die Matrix in eine 1×4n Matrix um, indem die Zeilen aneinandergehängt werden. Jetzt kann man über den errechneten Index auf den Schwächungskoeffizienten im entsprechenden Pixel zugreifen: si = SM(i). Wenn die Indizes in einem Vektor, zum Beispiel i abgelegt werden und damit auf die Schwächungsmatrix zugegriffen wird, dann liefert der obige Befehl auch einen Vektor mit den zugehörigen Koeffizienten zurück. Somit kann die Berechnung nach der Formel (2) für einen Strahl, dessen durchlaufene Pixel bzw. deren Index im Vektor b und die entsprechenden Längen im Vektor l liegt, folgendermaßen implementiert werden: Iout = exp(sum(-SM(b).*l))*Iin. Der angegebene Befehl funktioniert auch, wenn b und l Matrizen sind. Jede Zeile der Matrix entspricht dann dem Index- bzw. Längenvektor für einen Strahl aus dem Bündel. Das erhaltene Iout ist nun keine reelle Zahl mehr, sondern ein Spaltenvektor, der die Austrittsintensitäten für jeden Stahl enthält.

Für die weitere Implementation ist die Vorgabe einer Schwächungsmatrix notwendig. Dazu wurden die Hilfsprogramme »make_scross.m« und »make_object.m« (vgl. A.4 und A.2) entwickelt. Ersteres erzeugt eine quadratische Matrix angegebener Größe und besetzt sie so, daß der entstehende Querschnitt wie ein Schweizer Kreuz aussieht.

Das zweite Programm bietet die Möglichkeit ein Phantom mit Hilfe einer ,,graphischen Oberfläche'' zu erzeugen. Damit stehen verschiedenste Testobjekte zur Verfügung.

Die Simulation beginnt mit der Darstellung des Phantoms und der Strahlenquelle (vgl. A.3). Anschließend wird das Modul »spunkt.m« ausgeführt. Die Berechnung der Austrittsintensitäten für das aktuelle Bündel erfolgt wie beschrieben. Die Strahlenquelle wird um den Winkel auf dem Kreis weiterbewegt, so daß sich für ergibt. Der Algorithmus wird solange wiederholt, bis die Quelle einen vollen Kreis beschrieben hat. Die errechneten Intensitäten werden zwischengespeichert und können so später weiterverwendet werden.

Abbildung 8: Schwächungskurve

Betrachtet man Abbildung 8 auf Seite pageref so zeigt sich die Abhängigkeit der Austrittsintensität von der Auslenkung des Zentralstrahls, wobei hier nur die Schwächung desselben ausgewertet wurde. Das benutzte Phantom war ein "Schweizer Kreuz" mit n=2 (vgl. Abbildung 7). Man erkennt deutlich vier "Spitzen", das heißt es gibt Winkel unter denen die Abschwächung am geringsten ist. An diesen Stellen hat der Strahl die kürzeste Strecke unter Schwächung zurückgelegt. Diese "Spitzen" repräsentieren sozusagen die vier fehlenden Ecken des Phantoms. Die Kurve beschreibt den Aufbau des untersuchten Objekts. Die Rekonstruktion eines Bildes aus diesen Meßdaten ist Thema des nächsten Abschnittes.

Das direkte Problem hat uns bei der Einarbeitung in die Materie geholfen. Wir erhielten so einen konkreten Einstieg in Matlab und schufen gute Voraussetzungen für das anstehende inverse Problem.

Die Faktoren kommen darin nur linear vor. Man könnte also aus n solchen Gleichungen ein lineares Gleichungssystem bilden, dessen Lösung die gesuchte Zusammensetzung liefert. Bei einer Auflösung von 20 × 20 ergeben sich 400 Unbekannte; es sind also 400 Gleichungen notwendig. Doch schon bei einer Schrittweite von step = 60 ( = 6°) und 9 Strahlen im Bündel erhält man 9·60 = 540 Gleichungen. Dabei stellt sich die Frage, warum bzw. step nicht so wählt wird, daß die Zahl der Gleichungen der Anzahl der Unbekannten entspricht. Diese Forderung ist technisch kaum umzusetzen und würde die Messung nur unnötig verlängern. Außerdem ergeben sich durch mehr Gleichungen verschiedene Vorteile bei der Bildrekonstruktion (vgl. Inverses Problem - Probleme).

Man benötigt somit ein Verfahren um überbestimmte Gleichungssysteme lösen zu können. Ein weiteres Problem ist die Dimensionierung des gewünschten Bildes, denn schon die Verdopplung der Auflösung bedeutet eine Vervierfachung der Anzahl an Unbekannten und damit auch eine deutliche Erhöhung des Rechenaufwandes (vgl. Inverses Problem - Probleme).